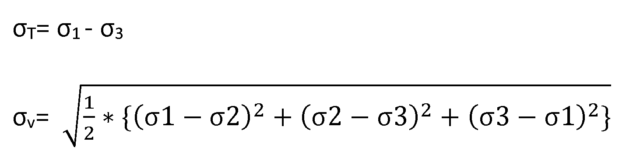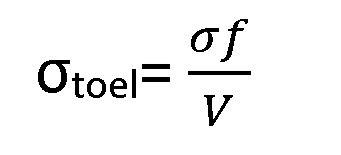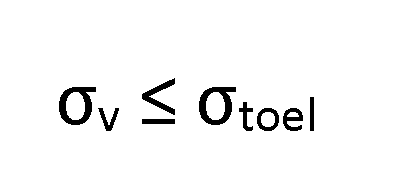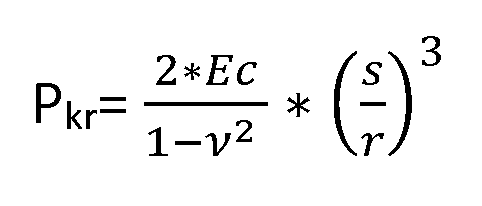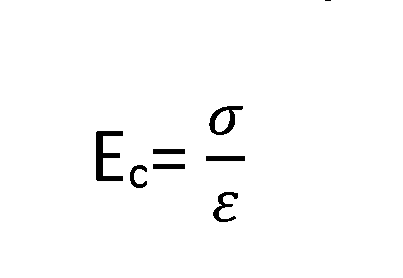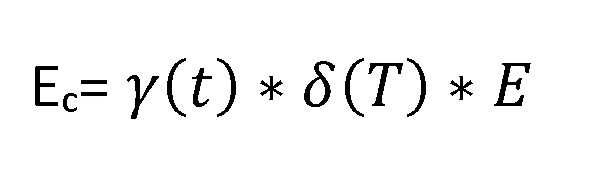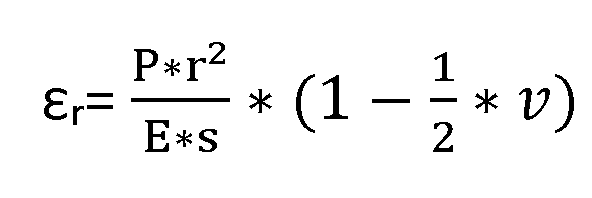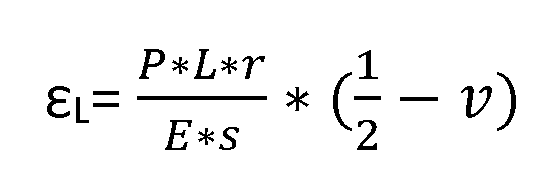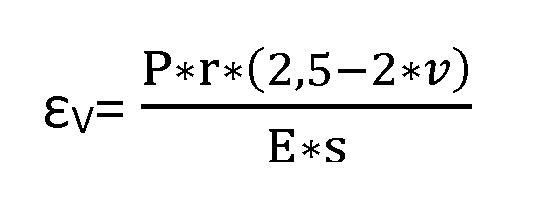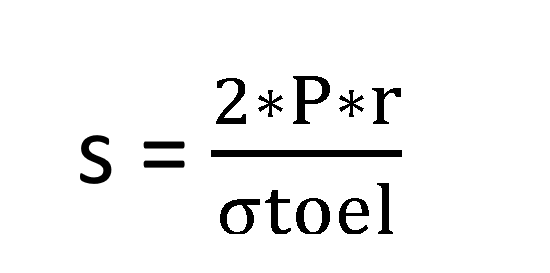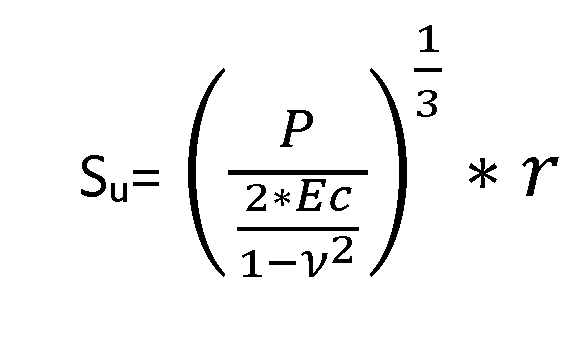Sterkteberekening

Om pijpleidingsystemen te ontwerpen moet er een sterkteberekening uitgevoerd worden door een piping engineer. Hier zullen we uitleggen welke krachten er op een pijpleiding werken en waar je rekening mee moet houden tijdens het ontwerp.

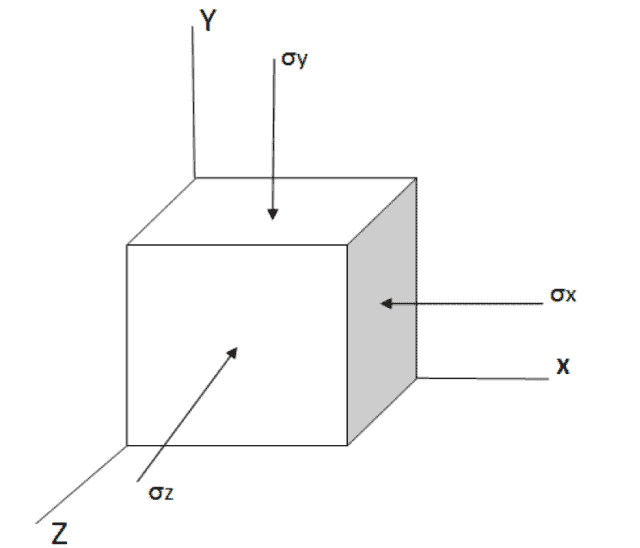
Er zijn verschillende typen krachten die op een lichaam kunnen werken. Spanning is een gemiddelde die gedefinieerd wordt door de kracht die inwerkt op een lichaam gedeeld door de oppervlakte waarop die kracht werkt. Bij het analyseren van de spanningen in een materiaal kan de spanningstoestand benaderd worden met een kubus, waarop de volgende spanningen werken:

Uit deze kubus kunnen de 3 hoofdspanningen σx, σy en σz gehaald worden.

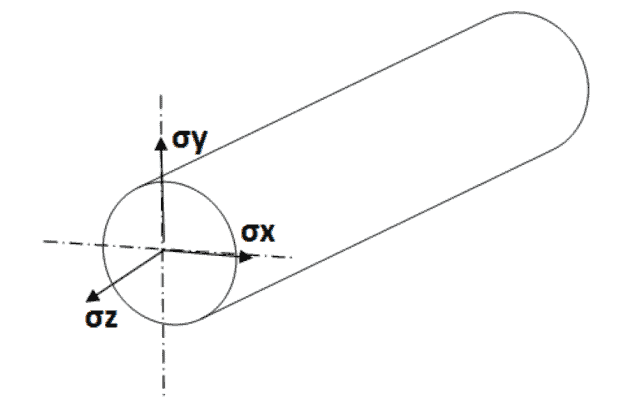
Voor een cilinder die belast wordt door drukspanningen kunnen de hoofdspanningen als volgt analyseert worden:

Om een sterkteberekening uit te voeren voor drukbuizen/vaten wordt de formule van Barlow toegepast. Deze formule is afgeleid van de ‘ketelformule’. In de ketelbouw zijn er twee groepen vergelijkingen, namelijk dunwandig en dikwandig cilinders. De grens ligt hiervoor bij d=1/8 D, dus als d<1/8 D gaan we uit van dunwandig, anders wordt de leiding als dikwandig beschouwd. Hierin staat d voor de wanddikte en D voor de diameter. We gebruiken een dunwandig drukvat, omdat hierbij de wandspanningen constant zijn over de wanddikte. Dit resulteert in de volgende vergelijkingen om de spanningen uit te rekenen.

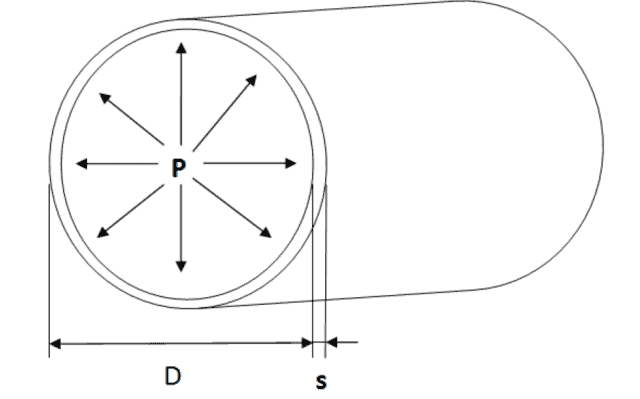
Voor een cilinder met open uiteinden geldt:

Hierin staat (P) voor de druk, (s) is de wanddikte en (D) is de binnendiameter.

Grensspanningscriteria sterkteberekening

Er zijn twee theorieën die de maximale spanning tot plastische vervorming voorspellen, namelijk Tresca(σT) en Von Mises (σv):

De Von Mises benadering is het meest gebruikte criterium bij een sterkteberekening die we verder zullen behandelen.

Bij de theorie van Von Mises wordt de vergelijkspanning uitgedrukt in drie hoofdspanningen, waardoor een assenstelsel onafhankelijk beschrijving verkregen wordt.

Om de grensspanningscriteria theorieën te begrijpen gaan we een stuk dieper in op de trekproef van een materiaal.

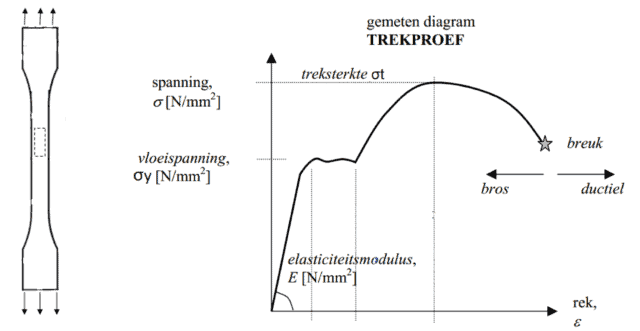
Bij een trekproef wordt een genormeerd vormgegeven proefstaaf opgerekt tot er breuk optreedt. De proef kan bij verschillende temperatuurverschillen worden uitgevoerd en geeft dan informatie over het materiaalgedrag bij die temperatuur. De trekproef is een belangrijke proef die veel product parameters oplevert. De staaf wordt aan de uiteinden met twee klemmen ingeklemd en opgerekt. Door het dunner maken van de staaf in het midden voorkom je dat het breekt bij de ingeklemde stukken. Tijdens het uitrekken wordt de oprekking en de kracht gemeten. De uitkomsten worden weergegeven in een diagram:

De σy is de aanduiding voor de maximale spanning van het materiaal, wanneer een spanningstoestand groter is dan de vloeispanning dan zal er plastische deformatie optreden.

De treksterkte van een materiaal wordt gebruikt als een maatstaaf om de mechanische eigenschappen van een materiaal te classificeren. Praktisch is de vloeigrens van een materiaal veel meer van belang. Als het materiaal tot de treksterkte komt, is het materiaal al sterk plastisch vervormd. Als ontwerper ga je nooit boven de vloeigrens σy dimensioneren bij een sterkteberekening.

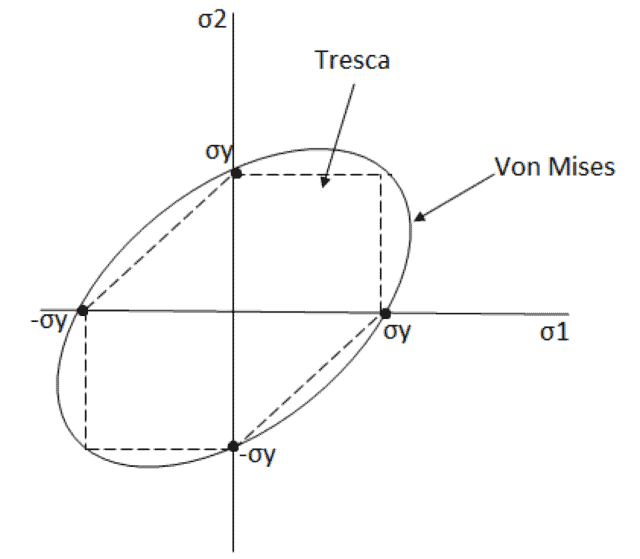
Als we de spanningen σ1 en σ2 gaan plotten in een grafiek dan krijgen we het volgende, waarbij σ3 nul is:

Als de Tresca spanning binnen de polygon valt en de Von Mises spanning binnen de ellips valt dan voldoet het materiaal en treedt er geen vervorming op. Buiten de polygon en ellips zal er plastische deformatie optreden, waardoor het materiaal bezwijkt.

Toelaatbare spanning

Om te voorkomen dat het materiaal blijvend vervormt, wordt er als veiligheid een toelaatbare spanning gebruikt bij een sterkteberekening. De toelaatbare spanning wordt bepaald uit de faalspanning σf  of te wel σy (vloeigrens) door deze waarde te delen door een veiligheidscoëfficiënt V.

In formulevorm is de toelaatbare spanning:

De berekende grensspanning of Von Mises spanning mag op enige plaats in het product ten hoogste gelijk zijn aan de toelaatbare spanning.

De veiligheidscoëfficiënt is een verantwoordelijkheid van de ontwerper. Hij moet de vereenvoudigingen en de niet kwantificeerbare verwerkingsinvloeden schatten. De grootte van de veiligheidscoëfficiënt kan ook vastgesteld worden door diverse instanties die geautoriseerd zijn door de overheid of door de overheid zelf.

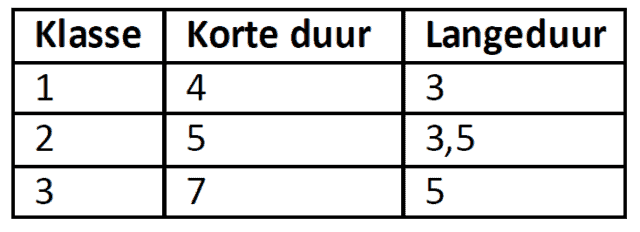
Voor leidingen en vaten die worden toegepast in de procesindustrie gelden veiligheidscoëfficiënten volgens norm VM 15 (Nederland) en DVS 2205 (Duitsland).

Men maakt onderscheid naar kans op gevaar voor personen en zaken

• Gevarenklasse 1

Rustende belasting bij kamertemperatuur, bij schade geen gevaar voor personen of zaken

• Gevarenklasse 2

Rustende belasting bij wisselende omstandigheden (temperatuur, valhoogte). Bij schade geen gevaar voor personen of zaken.

• Gevarenklasse 3

Wisselende belasting bij ruwe bedrijfsomstandigheden. Bij schade gevaar voor personen of zaken mogelijk.

Hieronder staan de veiligheidscoëfficiënten naar gevarenklasse:

Externe druk

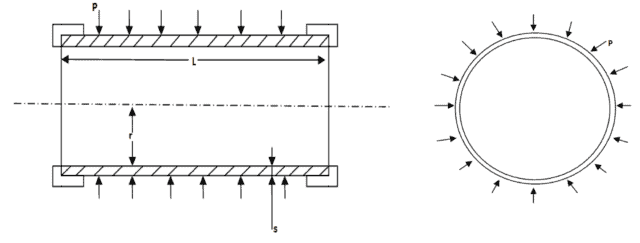
Bij externe druk of vacuüm kan een cilindrische buis bezwijken, waardoor de buis samen wordt gedrukt. De maximale externe druk die een dunwandige cilindrische buis met open uiteinden aan kan wordt ook wel de kritische deukdruk genoemd. In het Engels wordt de samendrukking aangeduid met ‘Buckling’.

Volgens de Euler buckling theorie geldt voor een dunwandige cilinder met open uiteinden voor de kritische deukdruk:

Kruipmodulus sterkteberekening

Kruip is een blijvende vervorming bij materialen dat gedurende langere tijd met een spanning belast is, meestal bij hoge temperaturen. Voor een lange duur gedrag kan met behulp van de levensduur-trekproef de kruipmodulus (Ec) worden bepaald.

De kruipmodulus is het quotiënt van de spanning (σ) en de uitzetting (ε):

Volgens DIN of ASTM norm kunnen we voor het langeduur gedrag een factor ƴ voor tijd en factor δ voor temperatuur nemen om de kruipmodulus te schatten op basis van de korte duur elasticiteitsmodulus (Ec):

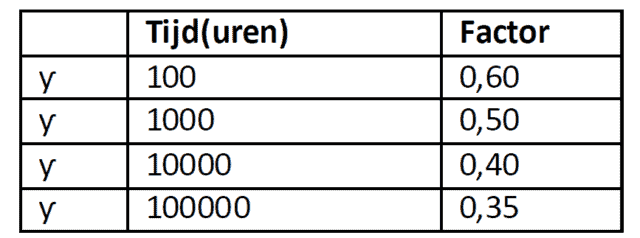
Voor thermoplasten geldt factor ƴ als functie van tijd:

Op de zelfde wijze kunnen we factoren δ aangeven, waarmee op temperatuur wordt gecorrigeerd:

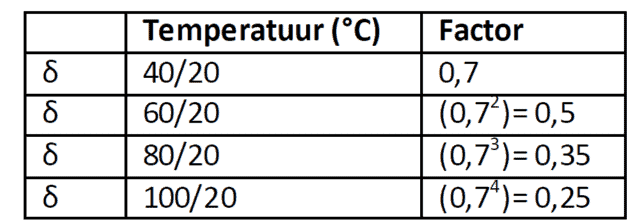
Voor thermoplasten geldt factor δ voor temperatuur:

Met deze benaderingen wordt de kruipmodulus Ec voor kunststoffen bij een bepaalde belastingsduur en bij een bepaalde temperatuur gegeven door:

Spanning rek-relaties sterkteberekening

Bij lineair-elastische materialen wordt de spanning-rek relatie gegeven door de Wet van Hooke. Door het toepassen van de Wet van Hooke kunnen we de toename in de inwendige straal, toename in verlening en verandering van het volume van een cilindrische buis berekenen aan de hand van de druk.

Toename inwendige straal

Toename verlening van de buis

Verandering van het inwendige volume van de buis (volume rek)

Hierbij is (P) de druk, (r) is de straal, (v) is de dwarscontractiefactor, (E) is de elasticiteitsmodulus en (s) is de wanddikte

Temperatuurspanningen in sterkteberekening

Temperatuurspanningen ontstaan in lichamen waar de vrije uitzetting of inkrimping bij een temperatuur wijziging belemmerd wordt. Deze spanningen kunnen zeer groot worden en zijn dikwijls de oorzaak van overbelasting en breuk.

De thermische uitzetting is gemakkelijk te berekenen aan de hand van de volgende formule:

ΔT wordt bepaald door de referentie temperatuur(kamertemperatuur 20°C) af te trekken van de maximale optredende temperatuur. (L) is de lengte van de buis en (α) is de lineaire uitzettingscoëfficiënt.

Minimale wanddikte

De minimale wanddikte van een cilindrische buis dat belast wordt door interne druk kan je afleiden uit de Ketelformule en wordt gegeven door:

Bij externe druk kan je de minimale wanddikte afleiden uit de Euler formule en dat wordt gegeven door:

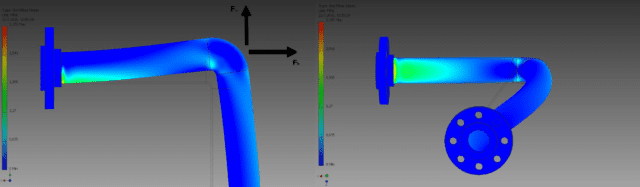
FEM analyse pijpleiding

De laatste tijd is FEM analyse de meest gebruikte methode voor het oplossen van technische en wiskundige modellen. Met behulp van eindige-elementenmethode of FEM wordt een fysiek fenomeen gesimuleerd om het echte gedrag te analyseren. Veel piping engineers gebruiken standaard design software voor pijpleidingen die voor complexe situaties geen sterkteberekening kunnen uitvoeren. Hierbij moet een FEM analyse uitgevoerd worden. HIGTEC kan voor u een FEM analyse uitvoeren voor elke soort situatie.